Smith-Waterman Algorithm: Local Alignment

5. Smith-Waterman Algorithm: Local Alignment#

5.1. Background#

Developed by Temple F. Smith and Michael S. Waterman in 1981, the Smith-Waterman algorithm is the classical method for forming local sequence alignments[SW81]. It was designed to identify regions of similarity within long sequences of DNA, RNA, or proteins, allowing for variability in length and composition.

5.2. Principle#

The Smith-Waterman algorithm employs dynamic programming to construct an alignment matrix that scores local alignments between two sequences. It initializes the matrix and fills it based on match, mismatch, and gap penalties, iteratively computing the highest possible score for any contiguous alignment segment.

5.3. Implementation#

The implementation of the Smith-Waterman algorithm involves initializing an alignment matrix with zeros, and then iteratively updating its cells based on the scores of adjacent cells and the scoring schema (match, mismatch, and gap penalties). Key considerations include the choice of scoring parameters and the method for traceback to reconstruct the optimal local alignment.

5.4. Applications#

The Smith-Waterman algorithm is crucial for various applications in genomic research, drug discovery, and evolutionary studies. It is particularly useful in situations where the most informative element is a portion of the available data, such as identifying conserved motifs within a larger genomic sequence or aligning sequences that include regions of high variation.

5.5. The definitions of the problem, and the solution#

Given two sequences \(a_1,\ldots,a_N\) and \(b_1,\ldots,b_M\), a scoring function \(d(x,y)\), find a local alignment that gives an optimal (maximal) score.

The solution can be found by studying the dynamic programming matrix, \(S\), of size \((N+1,M+1)\), by using the recursions defined in equations (5.1) and (5.2).

(5.1)#\[\begin{split}\begin{align*} S_{0,0} = 0, & \\ S_{i,0} =& 0, & \textrm{for all}\ i \\ S_{0,j} =& 0, & \textrm{for all}\ j \end{align*}\end{split}\]

(5.2)#\[\begin{split}S_{i,j}=\max \begin{cases} 0\\ S_{i-1,j-1} & + d(a_i,b_j)\\ S_{i-1,j} & + d(a_i,-)\\ S_{i,j-1} & + d(-,b_j). \end{cases}\end{split}\]

5.6. Example#

Here is an example alignment of the sequences GAC and ACG using Smith-Waterman, when we have a scoring function, \(d(x,y)= \begin{cases}1 & \textrm{if} x=y\\ -1 & \textrm{otherwise } \end{cases}\).

We start by filling in the borders of the matrix using Equation (5.1), as shown in Fig. 5.1.

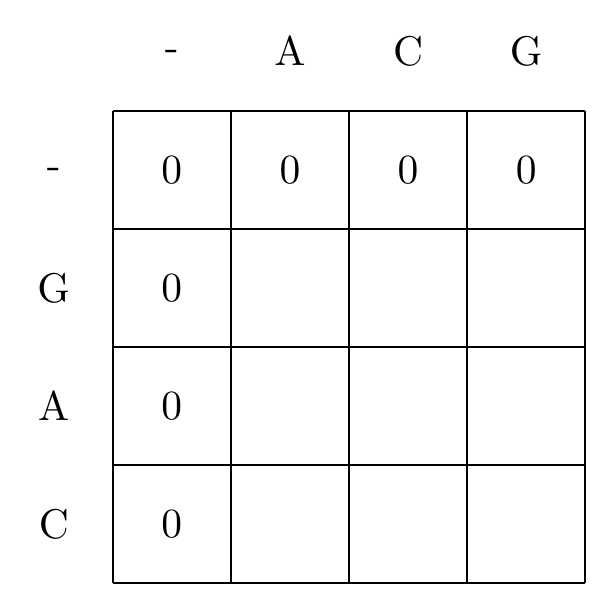
../_images/sw_short_init.png — Fig. 5.1 Initialization of the dynamic programming matrix, using using Equation (5.1). For Smith-Waterman this equates to setting the elements of the first row and column to 0.#

We then recusively fill in the other elements of the matrix in a row wise manner using Equation (5.2), as shown in Fig. 5.2.

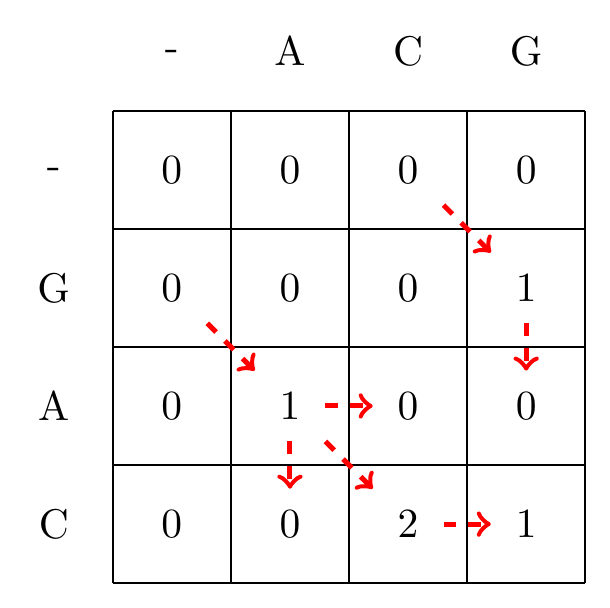
../_images/sw_short_fill.png — Fig. 5.2 Filling in the matrix. We fill in the elements recursively, in a row-wise manner. Each cell’s value is evaluated using Equation (5.2). We store trackers of which step we used to reach a certain cell, indicated by red arrows. Note that for some cells there are multiple optimal steps, i.e. paths that have the same score.#

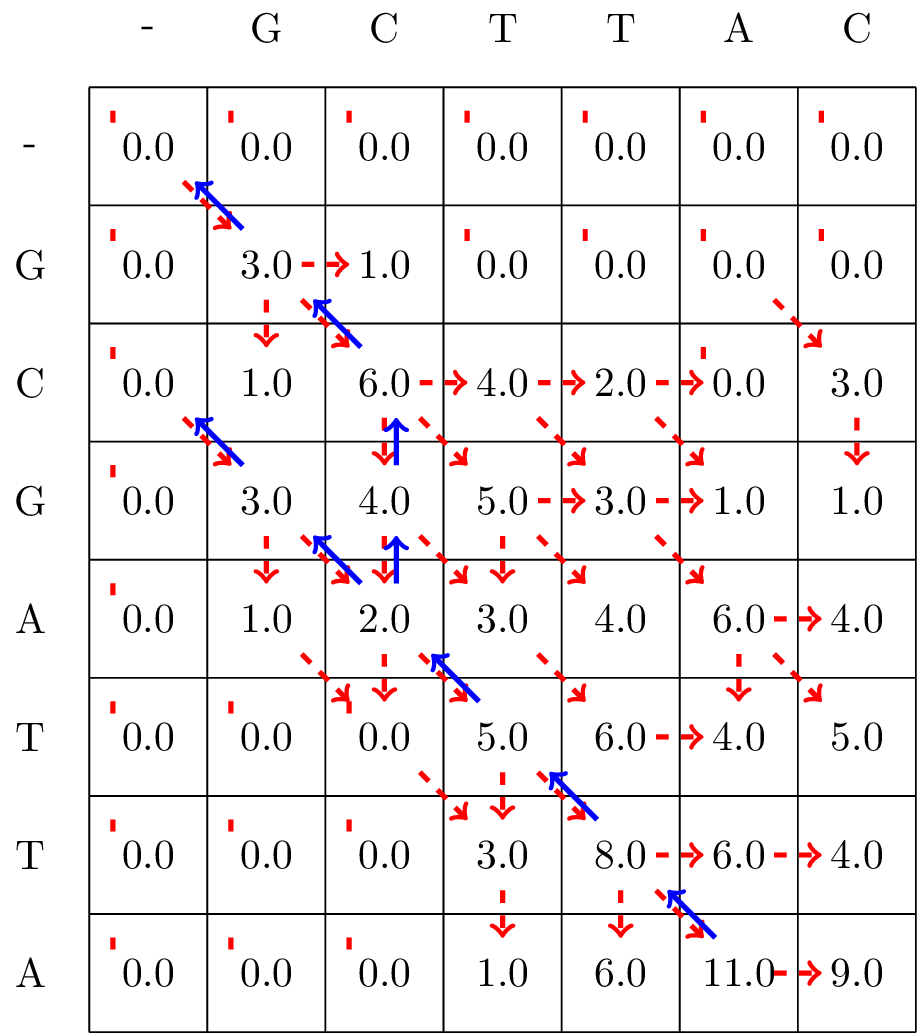
Given the filled in matrix, we can now track the optimal path from the bottom right element of the matrix, following the arrows back to the top-left element, as shown in Fig. 5.3.

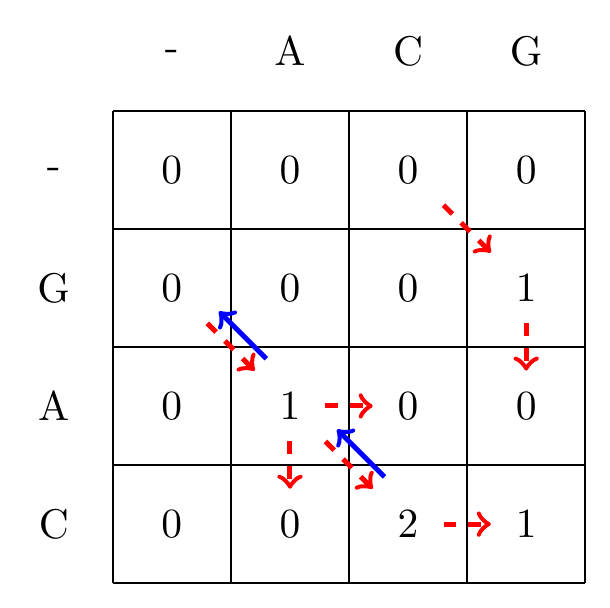
../_images/sw_short_bt.png — Fig. 5.3 We follow the alignment backwards from the matrix element with the largest value, \(\max_{i,j} S_{ij}\), to the first encountered cell with a value of zero, and mark the found optimal path with blue arrows.#

5.6.1. Exercises#

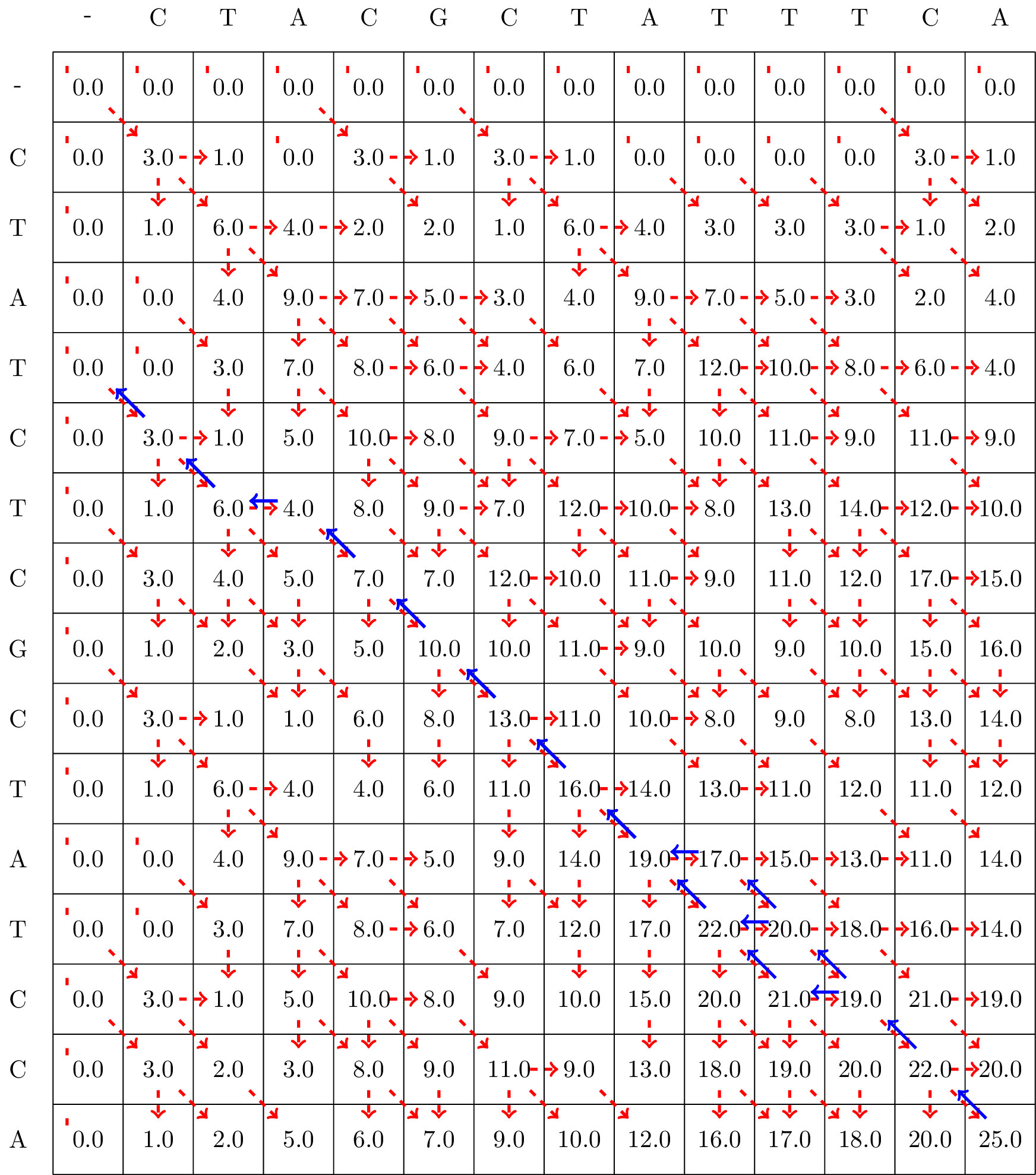
Exercise 5.1 (Smith-Waterman Alignment 1)

Calculate the Smith-Waterman Alignment of the following two sequences:

GCGATTA   
GCTTAC

Use the following scoring scheme:

Match: +3
Mismatch: -1
Gap penalty: -2

Exercise 5.2 (Smith-Waterman Alignment 2)